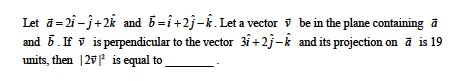For the reaction $2NO_2 (g) \rightleftharpoons N_2O_4 (g) $, when $\Delta S = -176.0 JK^{-1} $ and $\Delta H = -57.8 kJ mol^{-1} $, the magnitude of $\Delta G $ at 298 K for the reaction is _ _ _ _ $kJ mol^{-1} $. (Nearest integer)
Solution
We have, $\Delta G = \Delta H – T \Delta S $
$\Delta S = -176.0 JK^{-1} = -0.176 kJ K^{-1} $
$\Delta G = -57.8 – 298 \times (-0.176) \approx -57.8+52.5 = -5.3 $
$\therefore |\Delta G | = 5.3 kJ mol^{-1} $
Ans: 5
The molar solubility of $Zn(OH)_2 $ in 0.1 M NaOH solution is $x \times 10^{-18} M$. The value of x is _ _ _ _ . (Nearest integer)
(Given: The solubility product of $Zn(OH)_2 $ is $2 \times 10^{-20} $)
Solution
$Zn{(OH)_2}\rightleftharpoons \mathop {Z{n^{2 + }}}\limits_s + 2\mathop {O{H^ – }}\limits_{2s + 0.1} $
${K_{sp}} = [Z{n^{2 + }}]{[O{H^ – }]^2} = s.{(2s + 0.1)^2}$
$\therefore 2 \times {10^{ – 20}} = s.{(2s + 0.1)^2} \approx {0.1^2} \times s$
$ \Rightarrow s = 2 \times {10^{ – 18}}$
$\therefore x = 2 $
An empty LPG cylinder weighs 14.8 kg. When full, it weighs 29.0 kg and shows a pressure of 3.47 atm. In the course of use at ambient temperature, the mass of the cylinder is reduced to 23.0 kg. The final pressure inside the cylinder is _ _ _ _ atm. (Nearest integer)
(Assume LPG to be an ideal gas)
Solution
Weight of gas before use = 29.0 – 14.8 = 14.2 kg
Weight of gas after use = 23.0 – 14.8 = 8.2 kg
Now, $\frac {P_1}{n_1} = \frac {P_2}{n_2} $
$\Rightarrow \frac {P_1}{w_1} = \frac {P_2}{w_2} $
$\therefore \frac {3.47}{14.2} = \frac {P_2}{8.2} $
$\Rightarrow P_2 = \frac {3.47 \times 8.2}{14.2} \approx 2 atm $
Answer: 2
If the conductivity of mercury at $0^\circ C $ is $1.07 \times 10^6 Sm^{-1} $ and the resistance of a cell containing mercury is $0.243 \Omega $, then the cell constant of the cell is $x \times 10^4 m^{-1} $. (Nearest integer)
Solution
$R=\frac {K_{cell}}{\kappa }$
Or, $K_{cell} = 0.243 \times 1.07 \times 10^6 \approx 26 \times 10^4 m^{-1} $
Answer: 26
Solution
The function f(x), that satisfies the condition $f(x) = x + \int\limits_0^{\pi /2} {\sin x.\cos yf(y)dy} $ is:
(A) $x + \frac{2}{3}(\pi – 2)\sin x$
(B) $x + (\pi + 2)\sin x$
(C) $x + \frac{\pi }{2}\sin x$
(D) $x + (\pi – 2)\sin x$
Solution
We have, $f(x) = x + \int\limits_0^{\pi /2} {\sin x.\cos yf(y)dy} = x + \sin x\int\limits_0^{\pi /2} {\cos yf(y)dy} = x + \sin x.k$
Where, $k = \int\limits_0^{\pi /2} {\cos yf(y)dy} = \int\limits_0^{\pi /2} {\cos y(y + \sin y.k)dy} $
$\therefore k = \int\limits_0^{\pi /2} {y\cos ydy} + k\int\limits_0^{\pi /2} {\cos y\sin ydy} $
$ \Rightarrow k = \left. {y\sin y} \right|_0^{\pi /2} – \int\limits_0^{\pi /2} {\sin ydy} + \frac{k}{2}\int\limits_0^{\pi /2} {sin2ydy} = \frac{\pi }{2} + \left. {\cos y} \right|_0^{\pi /2} – \frac{k}{2}.\frac{1}{2}\left. {\cos 2y} \right|_0^{\pi /2}$
$ \Rightarrow k = \frac{\pi }{2} – 1 – \frac{k}{4}( – 1 – 1) = \frac{\pi }{2} – 1 + \frac{k}{2}$
$ \Rightarrow \frac{k}{2} = \frac{\pi }{2} – 1 = \frac{{\pi – 2}}{2}$
$\therefore k = \pi – 2$
Now, $f(x) = x + \sin x.k = x + (\pi – 2)\sin x$
Answer: (D)
A 2 kg steel rod of length 0.6 m is clamped on a table vertically at its lower end and is free to rotate in vertical plane. The upper end is pushed so that the rod falls under gravity. Ignoring the friction due to clamping at its lower end, the speed of the free end of rod when it passes through its lowest position is _ _ _ _ $m s^{-1}$.
Solution
Decrease in gravitational potential energy = Increase in kinetic energy
So, $mgl = \frac {1}{2} I \omega ^2 = \frac {1}{2} .\frac {1}{3} ml^2 \omega ^2 $
$\Rightarrow 6g = l \omega ^2 $
Using $v = l \omega $, we have
$6 g = l. \frac {v^2}{l^2}$
$\Rightarrow v^2 = 6gl $
$\Rightarrow v = \sqrt {6gl} = \sqrt {6\times 10 \times 0.6 } = 6ms^{-1} $
Answer: 6